集中时间段
背景
事情是这样的。
我司最近要做一个定时报告功能,其中有一项是计算出一天 24 小时内,哪些时间段内出现告警的次数比较集中。 举个例子,下面是一天中从 0 点到 23 点,每小时出现的告警次数列表:
[25, 7, 5, 4, 10, 6, 17, 10, 10, 3, 6, 5, 6, 7, 2, 5, 2, 7, 0, 3, 0, 0, 1, 1]画成柱状图如下:
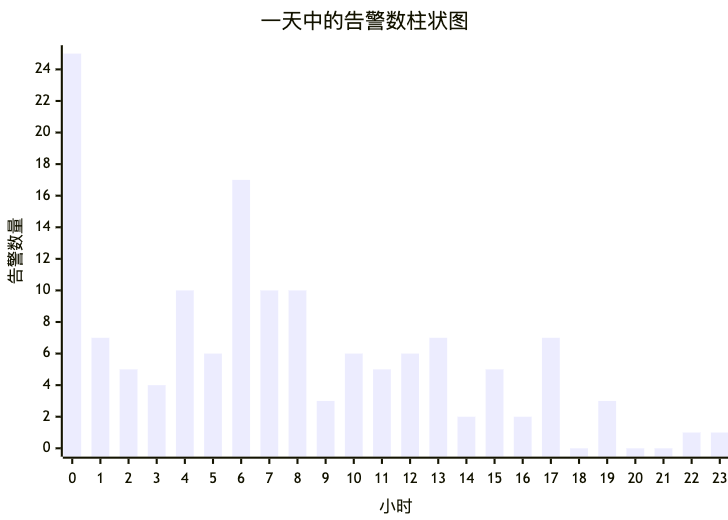
观察柱状图,我们可以随口一说
- 告警集中在 0 点到 17 点这段时间内(可是这都占一天时间的 了,集中个 P!)
- 告警集中在 0 点到 8 点这段时间内(好像说得过去?)
- 告警集中在 0 点到 1 点和 4 点到 8 点这两个时间段内(你觉得符合直觉吗?)
可以看到,具体怎么样才算集中,是相当主观的。
我想着,我应该不是第一个遇到这个问题的人,应该有现成的算法来搞这个东西。 于是问了下 deepseek,结果非常不满意。
想着现在可是 AI 新纪元了,这种事情就交给 AI 来搞好了!
AI 版算法
于是我写了个 prompt 让 AI 帮我来搞。如下:
你是一个高可用时间集中度分析器。请严格按以下步骤处理输入数据,最终输出必须是符合指定 JSON schema 的纯 JSON 对象,不要包含任何额外文本、解释或格式符号。
### 输入数据格式
- 24小时(0-23点)每个小时的告警数量数组,例如:`[5,0,3,...,12]`
### 集中时段判定规则
1. **连续时段**:仅考虑连续小时(时段长度≤4小时)
2. **总量阈值**:时段内告警总数 ≥ 全天告警总量的 40%
3. **数量限制**:最多 3 个时段,且时段不可重叠。如果两个时段是连续的,应当合并在一起。
4. **均匀分布时**:若无符合条件时段,输出空数组
### 输出要求
- 仅输出 JSON 对象,必须符合此 schema:
```json
{
"type": "object",
"properties": {
"timeSpans": {
"type": "array",
"items": {
"type": "object",
"properties": {
"start": { "type": "integer", "description": "从几点(包含)开始" },
"end": { "type": "integer", "description": "从几点(包含)结束。start 可以等于 end,表示集中于一个小时" },
"count": { "type": "integer", "description": "表示这个时间段内的数量" }
},
"required": ["start", "end", "count"],
"additionalProperties": false
}
}
}
}
`` `
- 示例输出:`{"timeSpans": [{"start": 9, "end": 11, "count": 35 }, ...]}`
### 处理流程
1. 计算全天告警总量 `totalAlerts`
2. 扫描所有连续时段(长度 1-4 小时),计算时段内告警和 `sum`
3. 若 `sum ≥ totalAlerts × 0.4` 则标记为候选时段
4. 按 `sum` 降序选取至多 3 个非重叠时段
- 连续合并: 如果两个区间是连续的,应当合并。比如有两个区间 {"timeSpans": [{"start": 17,"end": 18,"count": 28},{"start": 19,"end": 19,"count": 5}]}, 应当被合并为 {"timeSpans": [{"start": 17,"end": 19,"count": 33}]}
5. 若无合格时段,输出 `{"timeSpans": []}`
### 参考样例1
-> 输入:
- 0 点有 0 个
- 1 点有 0 个
- 2 点有 0 个
- 3 点有 0 个
- 4 点有 0 个
- 5 点有 0 个
- 6 点有 0 个
- 7 点有 0 个
- 8 点有 1 个
- 9 点有 10 个
- 10 点有 12 个
- 11 点有 14 个
- 12 点有 16 个
- 13 点有 0 个
- 14 点有 0 个
- 15 点有 4 个
- 16 点有 10 个
- 17 点有 18 个
- 18 点有 20 个
- 19 点有 5 个
- 20 点有 0 个
- 21 点有 0 个
- 22 点有 0 个
- 23 点有 1 个
<- 输出1: { "timeSpans": [{ "start": 8, "end": 13, "count": 53 }, { "start": 15, "end": 18, "count": 52 }]}
<- 输出2: { "timeSpans": [{ "start": 9, "end": 12, "count": 53 }, { "start": 16, "end": 18, "count": 48 }]}
<- 输出3: { "timeSpans": [{ "start": 9, "end": 12, "count": 53 }, { "start": 16, "end": 17, "count": 28 }, { "start": 18, "end": 18, "count": 20 }]}
其中只有输出2是合格的:
- 输出1不合格, 因为区间1是[8,13], 8 点只有 1 个, 13 点只有 0 个, 在集中区间里占比过分低了;
- 输出2合格, 因为区间[9,12], 这4个小时的数量显著比周围高, 区间[16,18] 也显著比周围高;
- 输出3不合格, 因为区间[16,17]和[18,18]是连续的,应当合并为[16,18]
### 参考样例2
-> 输入:
昨天的告警数量是:
- 0 点有 1 个
- 1 点有 2 个
- 2 点有 3 个
- 3 点有 0 个
- 4 点有 1 个
- 5 点有 2 个
- 6 点有 3 个
- 7 点有 0 个
- 8 点有 1 个
- 9 点有 2 个
- 10 点有 2 个
- 11 点有 1 个
- 12 点有 1 个
- 13 点有 2 个
- 14 点有 3 个
- 15 点有 0 个
- 16 点有 1 个
- 17 点有 2 个
- 18 点有 2 个
- 19 点有 1 个
- 20 点有 0 个
- 21 点有 0 个
- 22 点有 0 个
- 23 点有 1 个
<- 输出1: {"timeSpans": [{"start": 0, "end": 2, "count": 6}, {"start": 13, "end": 14, "count": 5}]}
<- 输出2: {"timeSpans": [{"start": 2, "end": 6, "count": 6}, {"start": 9, "end": 14, "count": 5}]}
<- 输出3: {"timeSpans": []}
其中只有输出3是合格的: 从数据中可以看到 24 小时中大部分都有数据, 但是大部分数据变化都比较平缓(所有数据取值都在 0-3 之间),所以没有集中趋势。于是我得到了一个计算集中时段的“算法”。
从 prompt 内容可以看出,AI “计算”这种东西的时候,总是出一些问题:
- 输出不稳定,同样的输入,经常会得到不一样的输出。
- AI 给出的集中时间段区间,可能包含两个紧挨在一起的区间,AI 又不会主动去合并。
现在这个情况不慎理想,是因为使用的是基础模型。除了上面两个比较严重的问题之外,还有些其他细微问题就不啰嗦了。 现在一次计算用时在 10s 左右。如果使用推理模型,一次“计算”的用时基本要 1 分钟以上。一个报告里要计算 5-8 次,这个时间消耗有点让人无法接受。
我就想有没有别的办法,但是连续几周,我都没有头绪,先用基础模型凑合吧。
手算版算法
前几天突然想到一个办法。
思路
是这样的:
每次都选取序列中最大的值,把它合并到附近“区间”中。如果附近没有区间,就让最大值单独成为区间。
下面是一个模拟的计算过程:
// 初态
[25, 7, 5, 4, 10, 6, 17, 10, 10, 3, 6, 5, 6, 7, 2, 5, 2, 7, 0, 3, 0, 0, 1, 1]
// 选取最大值 25,它周围没有区间,所以单独成区间
[[25], 7, 5, 4, 10, 6, 17, 10, 10, 3, 6, 5, 6, 7, 2, 5, 2, 7, 0, 3, 0, 0, 1, 1]
// 选取最大值 17,它周围没有区间,所以单独成区间
[[25], 7, 5, 4, 10, 6, [17], 10, 10, 3, 6, 5, 6, 7, 2, 5, 2, 7, 0, 3, 0, 0, 1, 1]
// 选取最大值 10,它周围有区间就加入,没区间就单独成为区间
[[25], 7, 5, 4, [10], 6, [17, 10, 10], 3, 6, 5, 6, 7, 2, 5, 2, 7, 0, 3, 0, 0, 1, 1]
// 选取最大值 7,它周围有区间就加入,没区间就单独成为区间
[[25, 7], 5, 4, [10], 6, [17, 10, 10], 3, 6, 5, 6, [7], 2, 5, 2, [7], 0, 3, 0, 0, 1, 1]
// 选取最大值 6,它周围有区间就加入,没区间就单独成为区间
[[25, 7], 5, 4, [10, 6, 17, 10, 10], 3, [6], 5, [6, 7], 2, 5, 2, [7], 0, 3, 0, 0, 1, 1]
// 重复上面的过程重复上面的步骤,我们可以把整个列表都合并成一个区间(😱)。这并不是我们想要的结果, 所以需要选择一个合适的时机,让计算停止,避免把所有的数字都加入区间。 我想到了用中位数作为停止条件:对所有大于(不包含等于)中位数的数字重复执行上面的步骤。
对于上面的例子,中位数是 5,所以我们计算完 6 之后就停止,得到:
[[25, 7], 5, 4, [10, 6, 17, 10, 10], 3, [6], 5, [6, 7], 2, 5, 2, [7], 0, 3, 0, 0, 1, 1]我们把其中的区间留下,得到
[[25, 7], [10, 6, 17, 10, 10], [6], [6, 7], [7]]现在我们有几个选择:
- 取区间总和最大的前几个(比如前 2 个)
- 取区间总和占一天中的百分比大于某个阈值的几个(比如 20%)(我选的是这个,效果尚可)
- 甚至可以综合区间的长度来筛选
可以看到,我们得到了几个区间,这些区间内的告警数量,占一天中总的告警数量比重较大; 而它们的总长度不会超过半天。区间长度短、占比重又较大,算是“集中”吧。
这样的算法对变化平缓的数据,也是适用的,如果数据整体波动不大,或者没有明显的集中趋势,会得不到任何集中区间。比如:
[1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4]的中位数是 2.5。经过两轮集中后,我们得到这样一些区间:
[[3, 4], [3, 4], [3, 4], [3, 4], [3, 4], [3, 4]]这些区间占整体的比例过低,都被排除掉了。
这个算法并不算完美,比如:
- 是否有比中位数更适合作为停止条件的数值?
- 区间集中的过程停止后,是否有更好的选取区间的方法?
我不知道。从我写了几十个测试用例后发现,选取中位数,然后选取区间占总体比例超过 20% 的区间,效果还行。
下面是我写的一个 Java 版
代码
,没有做优化,不过也差不多了:
import java.util.ArrayList;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
public final class DenseSpans {
public static <E> Item.Value<E> value(double value, E extra) {
return new Item.Value<>(value, extra);
}
public sealed interface Item<E> {
final class Value<E> implements Item<E> {
public Value(double value, E extra) {
this.value = value;
this.extra = extra;
}
public double value;
public final E extra;
public double value() { return value; }
public E extra() { return extra; }
}
record Range<E>(LinkedList<Value<E>> values, double sum) implements Item<E> {
public Value<E> first() { return values.getFirst(); }
public Value<E> last() { return values.getLast(); }
public String rangeStr() {
if (values.isEmpty()) {
return "";
}
if (values.size() == 1) {
return values.getFirst().extra.toString();
}
return String.format("%s-%s", values.getFirst().extra, values.getLast().extra);
}
}
}
public static <E> List<Item.Range<E>> merge(List<Item.Value<E>> values) {
return merge(values, 0.2);
}
public static <E> List<Item.Range<E>> merge(List<Item.Value<E>> values, double factor) {
if (values == null || values.size() < 3) {
return List.of();
}
var median = calcMedian(values); // 算中位数
// System.out.printf("中位数 %f\n", median);
var sum = values.stream().mapToDouble(Item.Value::value).sum();
var doubles = values.stream()
.filter(item -> item.value() > median) // 筛选大于中位数的值(等于的也不要,只要大于的)
.map(it -> it.value).distinct()
.sorted((o1, o2) -> Double.compare(o2, o1)) // 倒序排序
.toList();
List<Item<E>> stage = values.stream().map(it -> (Item<E>) it).toList();
for (var it : doubles) {
stage = mergeStage(stage, it);
}
return stage.stream()
.filter(item -> item instanceof Item.Range)
.map(it -> (Item.Range<E>) it)
.filter(it -> it.sum > sum * factor) // 筛选出占比超过 20% 的区间
.sorted((o1, o2) -> Double.compare(o2.sum, o1.sum))
.limit(3)
.toList();
}
private static <E> List<Item<E>> mergeStage(List<Item<E>> items, double value) {
// 把值大于或等于 value 的变成 Range
List<Item<E>> ranged = items.stream()
.map(it -> {
if (it instanceof Item.Value<E> iv) {
if (iv.value >= value) {
var list = new LinkedList<Item.Value<E>>();
list.add(iv);
return new Item.Range<>(list, iv.value);
}
}
return it;
})
.toList();
List<Item<E>> result = new ArrayList<>();
result.add(ranged.getFirst());
for (int i = 1; i < ranged.size(); i++) {
var curr = ranged.get(i);
var last = result.getLast();
if (last instanceof Item.Range<E>(LinkedList<Item.Value<E>> lastValues, double lastSum)) {
if (curr instanceof Item.Range<E>(LinkedList<Item.Value<E>> currValues, double currSum)) {
// 合并连续两个 range
var newValues = new LinkedList<>(lastValues);
newValues.addAll(currValues);
var newRange = new Item.Range<>(newValues, lastSum + currSum);
result.removeLast();
result.add(newRange);
} else {
result.add(curr);
}
} else {
result.add(curr);
}
}
return result;
}
private static final Comparator<Item.Value<?>> VALUE_DESC = (o1, o2) -> Double.compare(o2.value(), o1.value());
private static <E> double calcMedian(List<Item.Value<E>> values) {
var sorted = values.stream().sorted(VALUE_DESC).toList();
var size = sorted.size();
if (size % 2 == 0) {
return (sorted.get(size / 2 - 1).value() + sorted.get(size / 2).value()) / 2;
} else {
return sorted.get(size / 2).value();
}
}
}